Numerical diffusion of a passive scalar during a rotating base flow

The following animation shows the distribution of a passive scalar in a chronological sequence, whereas a level rotating base flow ( solid fluidized profile) was taken as a basis. A square “spot” (step function of the height) was chosen for the initial distribution. Since no physical diffusion effects are taken into account in the transport model, the spot should be carried along with the basic flow but ideally shouldn't change its shape.

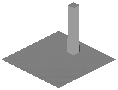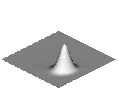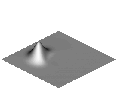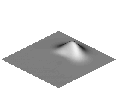
Due to the numerical diffusion, the form of the distribution does change during the calculation though. The way of discrediting the convective terms of the underlying transport equation is crucial for the strength of the numerical diffusion, which, like the physical diffusion, causes the spot to melt”.

In the following animations, the effects of the numerical diffusion for 3 different discretisation methods were compared. The grey-value images show the shape of the spot during a rotation in an isometric presentation. The colour images show the top view, whereby the respective height of the spot is represented by the colour (red=1, blue=0).

The calculations were performed with the 2-d Finite-Volume Code EBI-2d, which was developed at the Institute of Combustion Technology on a computational grid of 200*200 nodes. The courant number of all grid cells was smaller than 0,5.

You can klick on an animation to enlarge the view.
 

Hybrid-Verfahren	MLU-Verfahren n. Noll	SLIC-Verfahren